Part 1 – Time Value of Money of this series covered a basic introduction to the concept of compounding and looked at IRR and NPV in detail.
Here in Part 2, we pick up from there and examine XIRR, XNPV and the relationships of all these formula. We also look at NPV Factor and Days360.
The excel worksheet accompanying this post is available in Part 1 of the series or can be downloaded from here again:
[download_after_email id=”1979″]
5. Extended Internal Rate of Return
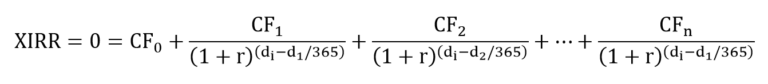
where:
r = Effective Rate of Interest
The problem with IRR formula is that it can only give the Annual Nominal Rate when the cash flows are evenly spread across many months. But it does not help if the cash flows are spread unevenly on different dates.
XIRR allows us to do that. Combined with the NOMINAL() function, we get the IRR!
Please see cell R14 just above the XIRR in cell R15.
Fun Fact: One interesting observation is if you change the start date from 01 January 2021 to 01 January 2020 the XIRR will change. I first created this excel with 01 January 2020 and just could not understand why the rate was not coming to 10.47%. It took me a while to understand that the year 2020 was a leap year and had 366 days which was reducing the effective rate. What I want to stress is, that even after years of practice, you will keep on getting confused but if you understand the fundamentals well, you will eventually be able to reconcile.
Additional reference material
6. Extended Net Present Value
XNPV solves the same problem with NPV as XIRR solves for IRR.
You will notice a interesting difference though.
In NPV we do not include the first row of outflow. If there is a inflow on the same date as the outflow, it is separately added outside the NPV formula. We will see examples later. But for XNPV we include the first row also since that also includes the first reference date for the outflow from when the interest starts accruing.
7. NPV Factor and Days360
There will be many instances where we will not want to use the IRR, NPV, XIRR or the XNPV but will require to use a more generic compounding formula.
We will then resort to NPV Factor. In the formula for compound interest (P x (1+ i/n)^(n x t)) – P, the portion inside the inner bracket is also referred to as the NPV Factor.
Actually the formula we want to use here is:
(1+i/12)^(no of days / “days with the year divided in 12 periods”)
or to say in layman terms:
(1+i/12)^(“no of times compounding happens”)
a. NPV Factor using (1+i/12)^(no of days*12/365)
Let us have a look at Columns V, W, X and Y.
In the formula section (1+i/n) we are taking n = 12 which means we are compounding the interest 12 times in the year. So for the formula to work correctly we have to divide the year into 12 equal periods. Now since a standard year has 365 days, to get one compounding month we divide 365 by 12 and the result is 30.41667 which is a little more than 30.
So instead of writing (1+i/12)^(no of days / 30.41667) we write (1+i/12)^(no of days * 12/365)
b. NPV Factor using (1+i/12)^(no of days/360)
Please see cell X18, the resulting Future Value is 110,624.21
The FV increases because you are now compounding over 12.16 periods (365/30)
c. NPV Factor using (1+i/12)^12
This is done just to cross check and show you that for a year the compounding needs to happen 12 times. Needless to say that this works here because we have an exact one year period.
d. NPV Factor using (1+i/12)^(no of days/30) with DAYS360
This is an interesting one. The result is correct and it is so because we calculate the number of days using the function DAYS360() which considers a year to have 360 days. And with a 360 day year, a division by 30 gives us 12 which is the correct times we need to compound.
Fun Fact: For a very long time I handled the relationship for one of the largest global technology companies who used DAYS360 in their leasing deals.
8. Conclusion
What we have covered in the two parts of this Time Value of Money series should be good enough for understanding equipment leasing. These formulae help us understand how the time value of money works in practice.
Even the other formulas like PMT, NPER, PV, PPMT, IPMT etc. use the same underlying logic as explained above and should be easy to understand.
I would also like to reemphasize – the inter relationships between these formulae is something we will find very important.
Additional Reference Material:




Pingback: Time Value Of Money - Part I | Assetz
Pingback: Fractional Equipment Leasing - An Analysis | Assetz